Comment appréhender différents systèmes dynamiques au moyen d’un jeu.
Système dynamique, système chaotique, système de fonctions itérées, attracteurs et fractales. Toutes ces notions mathématiques sont souvent abstraites, et assez difficiles à assimiler. Cet article vise à leur donner un aspect concret, au moyen d’un jeu, afin d’observer leur intervention et de les comprendre.
Plan
- Description
- Jeu du Chaos
- A. Matériel
- B. Règles
- C. But
- D. Exemple avec Mathematica
- E. Experimentation
- Questions & Réponses
- Conclusion
- Sources
I. Description
Le Jeu du Chaos est, par définition, un jeu où différents systèmes dynamiques interviennent, comme le chaos et le système de fonctions itérées, ou bien encore des notions comme les attracteurs et les objets fractals. Il fait référence à un moyen ordinaire de créer une fractale, en utilisant un polygone, et un point au hasard. La fractale est créée en trouvant un point résultant d’une fraction de la distance entre le point précédent, et l’un des trois sommets tiré au hasard, un grand nombre de fois.
Ce jeu fait également référence à un moyen relativement clair de générer et de mieux concevoir un attracteur ou un point fixe, et un système de fonctions itérées, en partant de règles qui font pourtant croire à une simple intervention du hasard.
Pour comprendre l’intérêt de ce jeu, il faut avant tout rappeler les systèmes dynamiques intervenants, la notion d’attracteur, ainsi que les objets dits « fractals ».
Un système dynamique appelé « chaotique » est un système sensible aux conditions initiales, et qui présente en même lieu une forte récurrence. Ces deux conditions provoquent un comportement dépourvu d’ordre, propre à son terme.
On dit qu’un système est sensible aux conditions initiales lorsque deux valeurs initiales extrêmement proches donnent des comportements complètement différents. Ces systèmes sont donc très sensibles aux perturbations.
L’exemple de système sensible aux conditions initiales le plus courant est celui de l’effet papillon. On dit que le simple battement d’aile d’un papillon en Australie peut entraîner une tempête sur la côte américaine. En d’autres termes, une perturbation minime, comme celle de ce papillon, a des répercutions immenses sur le plan atmosphérique.
B. Système de fonctions itérées
Un système de fonctions itérées est une théorie mathématique utilisée la plus souvent utilisée dans la géométrie fractale. Il s’agit d’itérer, soit de répéter, aléatoirement des fonctions dans un très grand nombre de fois, afin d’observer des attracteurs.
Nous pouvons illustrer ce système par un exemple assez explicite, en itérant la fonction de la « tente ». L’image parle d’elle-même ; on passe un point dans la fonction, et le résultat obtenu est lui-même utilisé et passé dans la même fonction.
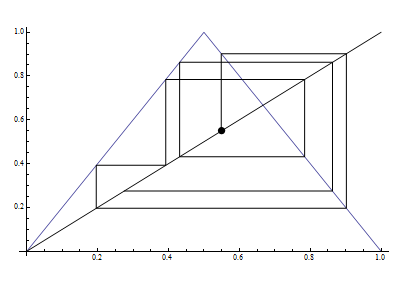
Un attracteur, dans l’étude des systèmes dynamiques, est un ensemble vers lequel un système de fonction est attiré de façon irréversible en admettant une absence de perturbation, d’où l’origine de son terme. Il s’agit le plus souvent d’un point ou d’une période.
Si l’attracteur possède une période de 3 ou de plus, l’application est forcément chaotique.
Comme exemple d’attracteur, nous pouvons reprendre la fonction de la tente, et itérer un point initial particulier afin d’obtenir un point fixe ou une période.

Il existe aussi l’attracteur défini comme étant étrange, découvert par Lorenz, qui forme deux magnifiques ailes de papillons.
La géométrie dite « fractale », inventée et découverte par Benoît Mandelbrot, possède une particularité géométrique particulière : la similitude interne. En d’autres termes, si nous agrandissons une petite partie d’une forme fractale, nous retrouvons une structure similaire à la structure globale.
Il existe des exemples naturels de fractales, comme le chou romanesco, ou bien les alvéoles des poumons humains. Les exemples les plus connus sont sans doute le flocon de Koch ou bien la fougère de Barnsley.

Retour en haut
II. Jeu du Chaos
Maintenant que nous avons rappelé les notions qui agissent dans ce jeu, observons dans quelles mesures elles interviennent, afin d’en avoir une image concrète. Pour ceci, jouons au Jeu du Chaos.
Pour jouer au Jeu du Chaos, nous avons besoin d’une feuille de papier, d’un crayon, d’un dé et d’une règle.
- Dessiner sur la feuille de papier à l’aide du crayon, un triangle équilatéral, dont il faut numéroter les trois sommets ; s1, s2, s3.
- Poser un point P n’importe où sur la feuille.
- Lancer le dé :
- Si le résultat est de 1 ou 2, aligner le point P avec le premier sommet.
- Si le résultat est de 3 ou 4, aligner le point P avec le deuxième sommet.
- Si le résultat est de 5 ou 6, aligner le point P avec le troisième sommet.
- Placer un nouveau point P sur la moitié du segment formé par le précédent point P et le sommet, au moyen de la règle.
- Relier les deux points P ensemble.
- Répéter les trois dernières opérations.

Le but de l’opération est de savoir :
- S’il est possible de prédire les points et les itinéraires.
- S’il existe d’autres formes qui ont les mêmes caractéristiques.
- Quelle est l’intervention des systèmes dynamiques.
- Quelle est l’intervention du hasard.
La suite de l’article visera principalement à répondre à ces questions.
Voici le code Mathematica d’un exemple illustré. Nous avons, dans cet exemple, suivi les consignes que nous avons répétées 50 fois. Un fichier notebook comportant plus de détails est fourni à la fin de l’article.
Il existe davantage d’exemples animés et interactifs avec MathematicaPlayer sur le site de Wolfram Demonstrations Project, dont celui-ci
Pour répondre à ces questions, il faut avant tout expérimenter plusieurs fois ce jeu. Grâce à Mathematica, nous pouvons expérimenter en temps réel le Jeu du Chaos. Voici donc ce que nous obtenons après quelques parties :
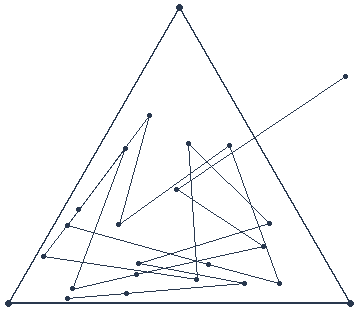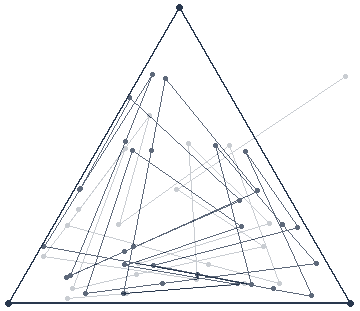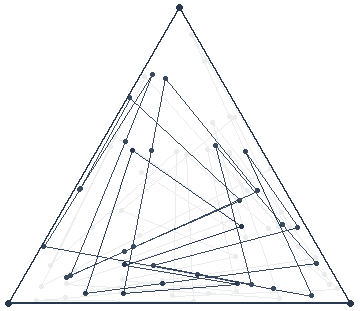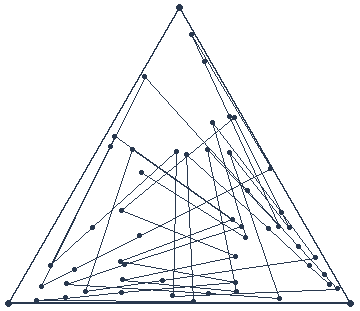
Si nous nous intéressons aux itinéraires obtenus entre les points P, nous pouvons pertinemment remarquer qu’il n’y a aucune relation logique. Ils sont donc totalement chaotiques. Nous expliquerons par la suite ce qui nous permet de l’affirmer. La seule chose que nous pouvons prédire à propos de ces itinéraires, c’est qu’ils rempliront entièrement le triangle après avoir itéré un grand nombre de fois.
Par conséquent, si nous nous intéressons uniquement au positionnement des points, c’est-à-dire que nous omettons la règle #5, nous obtenons le résultat suivant :
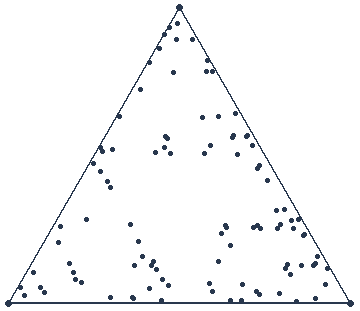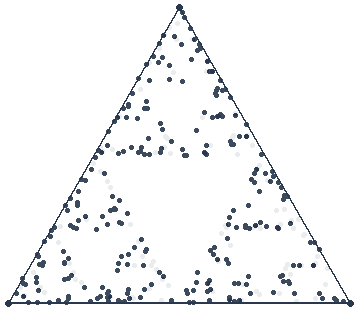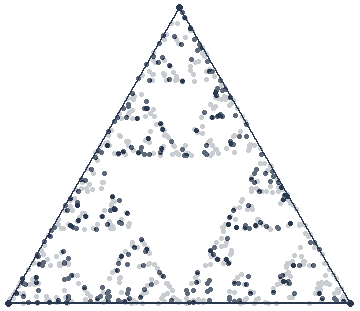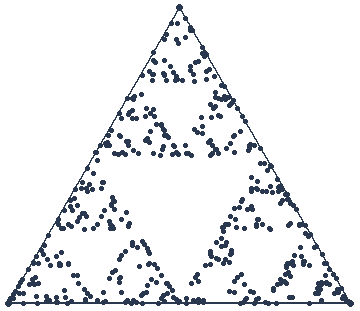
Et nous pouvons remarquer qu’il existe une certaine logique dans la position des points. Les attracteurs sont très distincts, et pouvons même prédire les zones inaccessibles aux points après un grand nombre d’itération.
Retour en haut
III. Questions & Réponses
Cette expérimentation a déjà apporté des premières impressions quant à la prévision après un certain nombre d’itérations.
– Attractions des itinéraires
Comme nous l’avions remarqué précédemment, il n’y a pas d’attracteurs pour les itinéraires, même après un grand nombre d’itérations ; c’est un système complètement chaotique. Pour avoir une certitude, itérons ce système de fonctions un grand nombre de fois - 50000, par exemple - sans cacher les itinéraires. Le résultat est flagrant :

Les itinéraires remplissent le triangle en intégralité après un grand nombre d’itérations. Ils ne possèdent pas de période d’attraction distincte, et donc ne sont en aucun cas prévisibles. De plus, il dispose des caractéristiques chaotiques, car il est sensible à la condition initiale, soit dépend du choix du premier point P, après une forte récurrence. Mais, nous nous y intéresserons plus tard, lors de l’intervention du hasard dans le choix du point initial.
– Attractions des points
Pour prédire les zones dans lesquelles les points ne peuvent, en théorie, pas accéder, il faut itérer ce système de fonctions un grand nombre de fois, comme nous l’avions fait pour les itinéraires. Le résultat est le suivant :

Nous obtenons donc bel et bien des attracteurs pour ces points ; des zones sont belles et bien épargnées, et d’autres sont belles et bien attractives.
En d’autres termes, après un grand nombre d’itération, les points ne pourront plus accéder aux zones épargnées, et atterriront toujours sur les zones d’attraction. Ces zones d’attractions sont les points fixes de l’attracteur de ce système de fonctions itérées. Grâce à ça, nous pouvons affirmer que la prédiction des points est absolument possible.
De plus, ces attracteurs forment la fractale du triangle de Sierpinski, forme particulière dont nous allons nous intéresser désormais.
– Formes
Nous avons vu que cela marche pour un triangle équilatéral. Essayons maintenant avec un triangle quelconque, et comparons le résultat quant aux attracteurs des points.

Nous remarquons que quel que soit le triangle que nous choisissons, nous obtiendrons à chaque fois une fractale après un grand nombre d’itérations. Le motif est juste "décalé" de celui de Sierpinski.
Cependant, le Jeu du Chaos ne dépend d’aucune autre forme que le triangle. Il est possible que d’autres formes admettent des attracteurs semblables au triangle de Sierpinski, mais au final, le motif obtenu ne sera pas une fractale.
– Sierpinski et son triangle
Wacław Franciszek Sierpiński était un mathématicien polonais, qui a contribué à la théorie des ensembles, à la théorie des nombres, à la théorie des fonctions et à la topologie.
En 1915, il construit les formes désormais connues, comme le triangle de Sierpinski (que nous avons vu précédemment) et le tapis de Sierpinski. Il s’agit de modèles mathématiquement générés qui peuvent être reproductibles à n’importe quel « zoom », qui porteront simplement le terme de fractales avec Mandelbrot en 1975.
Toutes les formes symétriques possèdent les caractéristiques fractales de Sierpinski, notamment le pentagone, l’hexagone, etc. Ces formes, cependant, ne peuvent pas être obtenues au moyen du Jeu du Chaos, pour une raison d’attracteurs et de zones épargnées. En effet, ces zones n’apparaissent pas avec la même harmonie que celles du triangle.
À première vue, ce jeu ne semblerait faire intervenir uniquement du hasard ; un choix du point d’origine aléatoire et un choix des sommets à aligner également aléatoire. Cependant, nous avons vu que le déterminisme des attracteurs prend le dessus après un grand nombre d’itérations. La question est de savoir en quoi le hasard influe dans ce jeu.
– Choix des sommets
Il faut garder à l’esprit que le point d’origine a une chance sur trois d’être relié à un sommet. Ceci est une proportion de chance. En effet, même en itérant 50000 fois, il est possible d’obtenir le même sommet à chaque fois. Heureusement, nous n’avons qu’une chance sur 1.5 · 105 que cela arrive. Et bien sûr, si cela arrivait, nous n’obtiendrons pas le motif de Sierpinski, mais un seul point. C’est pourquoi nous obtenons la fractale de Sierpinski en théorie seulement, même si cette précédente suite d’événements est insignifiante et très peu probable.
– Choix du point d’origine
Le positionnement des points ne dépend, en principe, pas du choix du point d’origine. Le hasard influe, en effet, pour - au maximum - les trois premiers points placés sur le triangle. En d’autres termes, les trois premiers points peuvent faire exception aux zones attractives. En effet, le Jeu du Chaos étant un système de fonctions itérées, le déterminisme des attracteurs ne fait effet qu’après un grand nombre d’itération seulement, comme nous l’avons défini au tout début.
Par conséquent, le choix du point d’origine dépend du positionnement des itinéraires. En effet, si nous prenons un point d’origine très proche d’un autre, nous observons que les itinéraires diffèrent complètement l’un de l’autre. De plus, comme le Jeu du Chaos est un système de fonctions itérées, et qu’il dépend du choix aléatoire des sommets - comme nous l’avons dit dans le point précédent - les itinéraires peuvent donc être différents avec un seul même point.
Les itinéraires sont donc bel et bien sensibles aux conditions initiales. Ils sont donc, comme nous l’avons défini, totalement chaotiques.
De plus, il est néanmoins nécessaire d’ajouter qu’il faut également prendre un point d’origine aléatoire dans le cadre du triangle, et non pas un point d’origine qui possède une portée infinie.
D. Intervention des systèmes dynamiques
Faisons donc un bilan de toutes ces interventions.
– Système chaotique
Le Jeu du Chaos possède les caractéristiques du système chaotique lors de la représentation des itinéraires entre les points, car ce système est sensible au point initial lors d’une forte récurrence et qu’il provoque un désordre absolu et irréversible.
– Système de fonctions itérées
En se basant sur les règles du jeu, on remarque qu’en définissant le choix des sommets comme étant trois fonctions que nous répétons à partir d’un point initial, le Jeu du Chaos est lui-même un système de fonctions itérées.
– Notion d’attracteurs
Tous les points du Jeu du Chaos sont attirés par des attracteurs, des zones dans lesquelles atterrissent tous les points, et les empêche ainsi d’accéder aux zones épargnées. Ces attracteurs forment après un grand nombre d’itérations, une fractale, celle du triangle de Sierpinski.
C’est grâce à toutes ces interventions de systèmes dynamiques que nous appelons ce jeu, « le Jeu du Chaos ». En effet, avec des moyens très basiques et des règles simples, nous avons pu découvrir et appréhender des théories mathématiques récentes et complexes.
Retour en haut
IV. Conclusion
Nous sommes parvenus à mettre le doigt sur des systèmes dynamiques physiques qui comporte des théories mathématiques assez complexes au moyen d’un jeu avec des règles claires. Nous pouvons conclure que le Jeu du Chaos possède une prédiction de points totalement possible, malgré l’intervention du hasard de l’expérience, mais que les itinéraires sont absolument chaotiques. De plus, nous avons trouvé un moyen de représenter une fractale.
Retour en haut
V. Sources
http://www.owl-spip.ch/
http://www.mathcurve.com/fractals/sierpinski/sierpinski.shtml
http://en.wikipedia.org/wiki/Chaos_game
http://fr.wikipedia.org/wiki/Sierpinski
Retour en haut
