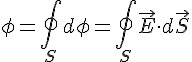Notion de flux et champ vectoriel - [S'informer et apprendre en ligne]

Flux

Notion de flux et champ vectoriel

Qu’est-ce qu’un flux ?

Première approche, explications, exemples et résolutions de problèmes...

Article mis en ligne le 2 mai 2006

dernière modification le 27 avril 2019

par Masami Sarumaru

La notion de flux est utilisée dans bon nombres de thèmes, que ce soit dans l’hydrodynamique, dans l’électromagnétisme, dans le chapitre de la chaleur ou autres. Ce travail comportera une première approche de cette notion, son explication (par des exemples), ses utilités et finalement, une présentation de l’un des outils qui aideront à la résolution de problèmes liés à ce sujet.

Première approche

" Le flux d’un champ vectoriel à travers une surface est la mesure du nombre de lignes du dit champ traversant cette surface."

Soit en d’autres termes : "Le flux est la quantité d’un ensemble d’éléments (énergie, matières, données, etc) évoluant dans un sens particulier à travers une surface".

La notion de flux est inséparable de la notion de champ.

Rappel : La notion de "champ" permet d’appréhender dans toute son étendue spatiale une perturbation (gravitation, température, pression, perturbation électrique et magnétique...). Ainsi, on appelle champ en physique une région de l’espace où en tout point on peut définir une grandeur. Si cette grandeur est scalaire (= un nombre)(champ de pression ou champ de température par exemple) on parlera de champ scalaire. Si la grandeur est vectorielle (= un vecteur) (champ électrique, champ de vitesse d’un cours d’eau) on parlera de champ vectoriel. La notion de champ est donc une fonction, scalaire ou vectorielle qui dépend des coordonnées de l’espace.

Quelques exemples :
– Le champ anémométrique est un champ vectoriel qui caractérise la vitesse du vent en tout point de l’espace.
– Le champ barométrique est un champ scalaire qui caractérise la pression en tout point de l’espace.
– Le champ de carottes de madame Durand est une approximation d’un champ vectoriel car il n’existe pas une carotte en tout point de son champ....

Exemples et explications

I. Flux en hydrodynamique

Le concept de flux a primitivement été introduit dans le cadre de l’étude de la dynamique des fluides. Le flux d’un liquide circulant dans un conduit est le débit de ce liquide à travers une surface fermée imaginaire, surface appelée "tube de courant".

1. Flux à travers une surface

Le débit est par définition le volume de liquide qui traverse chaque seconde une surface placée sur la trajectoire du courant. Dans le cas particulier où une surface plane S est perpendiculaire à un courant rectiligne, le débit se calcule de la façon suivante :

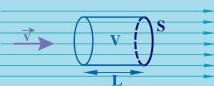
– Le volume est un cylindre de base S et de longueur L. $V=L \cdot S$
– La longueur est proportionnelle à la vitesse constante du liquide dans le tube.

$L=v \cdot t$

– Le débit se calcule alors de la façon suivante :

$D=\frac{V}{t}=\frac{L \cdot S}{t}=\frac{v \cdot t \cdot S}{t}=v \cdot S$

C’est le produit de la vitesse par la surface traversée par le courant.

Dans le cas plus général où la surface n’est plus perpendiculaire au courant, on définit un vecteur $\vec{S}$ normal à cette surface, dont la norme est égale à l’aire de la surface. Le débit devient alors le produit scalaire :

$D=\vec{v} \cdot \vec{S}$

Cette définition montre en particulier que le débit est nul lorsque $\vec{v}$ est perpendiculaire à $\vec{S}$ . Dans ce cas précis, la surface est parallèle aux lignes de courant, ce qui implique qu’aucun liquide ne la traverse.

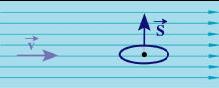
En hydrodynamique, la vitesse définit un champ vectoriel, dont les lignes de champ sont les lignes de courant. Le débit mesure donc l’écoulement du champ de vitesses $\vec{v}$ du liquide au travers de la surface .

Par extension, le flux est le débit d’un champ vectoriel au travers d’une surface.

2. Flux à travers une surface fermée

Dans le cas particulier où cette surface est fermée, le flux est directement relié aux sources du champ.

Une surface est dite fermée lorsqu’elle entoure un certain volume. Un tube de courant est une surface fermée dont les parois latérales sont parallèles et les bases perpendiculaires aux lignes de courant. Le liquide traverse alors deux surfaces différentes du tube, et . Le débit est ainsi séparé en un débit entrant () et un débit sortant ().

Par convention, $\vec{S}_1$ et $\vec{S}_2$ sont orientés vers l’extérieur du tube de courant, d’où :
– $D_1=\vec{v}_1 \cdot \vec{S}_1 =-v_1 \cdot S_1$ . Le débit du liquide entrant est négatif.
– $D_2=\vec{v}_2 \cdot \vec{S}_2=v_2 \cdot S_2$ . Le débit du liquide sortant est positif.

Le débit total à travers la surface fermée est la somme des débits entrant et sortant : =+. Il peut être nul, positif ou négatif, suivant les valeurs de et de :
– Si $|D_1|=|D_2|\Rightarrow D=0$ . Le débit entrant est égal au débit sortant. Il n’y a pas de source de liquide dans la surface S.
– Si $|D_1|<|D_2|\Rightarrow D<0$ . Le débit sortant est supérieur au débit entrant, il y a une source dans le volume délimité par la surface fermée. .
– Si $|D_1|> |D_2|\Rightarrow D >0$ . Le débit entrant est supérieur au débit sortant, il y a un puits dans le volume délimité par la surface fermée. .

Le débit à l’intérieur d’un tube de courant met en évidence les "sources" et les "puits" de liquide présents dans le volume délimité par une surface fermée.

Le flux d’un champ vectoriel au travers d’une surface fermée mesure donc les sources de champ présentes dans le volume délimité par cette surface.

II. Flux du champ électrique

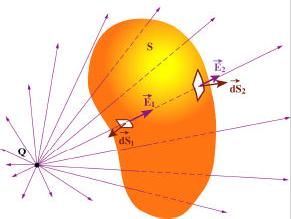
Le flux du champ électrique se calcule de la façon suivante :

On entoure une région de l’espace dans laquelle règne un champ électrique $\vec{E}$ d’une surface fermée .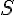
On découpe la surface 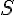en éléments de surfaces 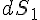, , 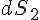... suffisamment petits pour que le champ électrique soit constant en grandeur et en direction au travers de ces éléments.
On définit le vecteur 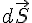avec les propriétés suivantes :
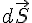- $d\vec{S}$ est perpendiculaire à la surface 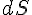. Il est orienté vers l’extérieur de .
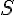- la norme de 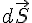$d\vec{S}$ est égale à l’aire de la surface .
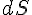Le flux des champs électrique 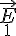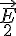$\vec{E}_1$ , $\vec{E}_2$ , ... au travers des éléments de surface 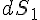, , 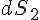... sont les produits scalaires suivants : $d \phi_1=\vec{E}_1 \cdot d\vec{S}_1$ , $d \phi_2=\vec{E}_2 \cdot d\vec{S}_2$ , ...
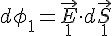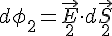Le flux total du champ électrique est la somme algébrique des éléments de flux 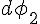$d \phi_1$ , $d \phi_2$ , ... sur toute la surface fermée : $\phi =d \phi_1+d \phi_2+...=\sum_{i}d \phi_i=\sum_{i}\vec{E}_i \cdot d\vec{S}_i$

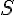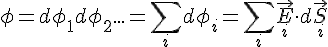
En fait, le champs $\vec{E}_1$ , $\vec{E}_2$ , ... ne sont constants que lorsque les éléments , , ... sont infinitésimaux. Dans ce cas précis, la surface est découpée en un nombre infini d’éléments de surface et le flux est une somme infinie de $d \phi_1$ , $d \phi_2$ , ... infiniment nombreux. La somme devient une intégrale :

$\phi=\oint_S d \phi=\oint_S \vec{E} \cdot d\vec{S}$

Le flux du champ électrique se calcule donc en toute rigueur avec les règles du calcul intégral.

Extension : Théorème de Gauss

Cette loi relie le flux du champ électrique au travers d’une surface fermée aux charges présentes dans cette surface. Elle s’écrit :

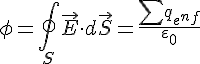$\phi =\oint_S \vec{E} \cdot d\vec{S}=\frac{\sum q_e_n_f}{\varepsilon_0}$ </math

$\sum q_e_n_f$ est la charge totale enfermée dans . La constante $\varepsilon_0=8,85 \cdot 10^-^1^2$ C est la permitivité du vide. Elle est reliée à la constante de la loi de Coulomb par la relation : $k=\frac{1}{4 \pi \varepsilon_0}$ . Cette loi est donc visiblement analogue à celle du débit d’un liquide dans un tube de courant, comme nous l’avons vu précédemment. Dans cette analogie, les charges positives sont les "sources" et les charges négatives les "puits" du champ électrique.

Outils de résolution de problèmes

Un des moyens pour calculer le flux d’un champ vectoriel sans en faire le calcul à la main est de schématiser la situation grâce au logiciel Mathematica.

Il faut tout d’abord définir le champ vectoriel dans lequel nous voulons calculer le flux :

m[x_, y_] := 0.4(y - 1);
n[x_, y_] := 0.1(x - 1);
v[x_, y_] := {m[x, y], n[x, y]}

A chaque point (x,y) du plan la fonction v(x,y) associe un vecteur.

Charger ensuite le module "Arrow".
Nous pouvons alors dessiner le champ ainsi que la surface à travers laquelle nous voulons voire la valeur du flux grâce à la formule suivante :

Needs["Graphics<code class="spip_code spip_code_inline" dir="ltr">Arrow</code>"]
xmin = -3; xmax = 3; ?x = 0.5;
ymin = xmin; ymax = xmax; ?y = ?x;
x[t_] := 1.5*Cos[t];
y[t_] := Sin[t];
tmin = 0; tmax = 2Pi; ?t = Pi/6;
orig = Flatten[Table[{x, y}, {x, xmin, xmax, ?x}, {y, ymin, ymax, ?y}], 1];
comp = Flatten[Table[{v[x, y]}, {x, xmin, xmax, ?x}, {y, ymin, ymax, ?y}], 2];
    
champ = {Hue[2/
      3], MapThread[Arrow, {orig, 
        orig + comp, Table[HeadScaling -> Relative, {Length[orig]}]}]};
courbe = ParametricPlot[{x[t], 
y[t]}, {t, 
    tmin, tmax}, PlotStyle -> {Hue[
        1/3], Thickness[0.005]}, DisplayFunction -> Identity];
Show[courbe, Graphics[champ], Axes -> 
          None, AspectRatio -> Automatic, DisplayFunction -> $DisplayFunction]

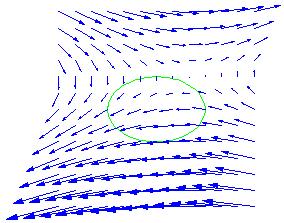
Nous n’avons besoin ici que des vecteurs touchant la courbe :

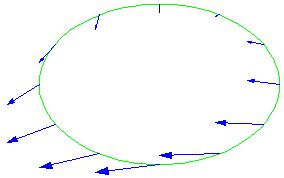
Les composantes du champ tangentes à la courbe définissent la "circulation" du champ sur la courbe (appelée parfois flux du champ sur la courbe). Les composantes du champ perpendiculaires à la courbe, appelées aussi composantes normales à la courbe, définissent le "flux" du champ à travers la courbe. Cherchons donc les composantes perpendiculaires à la courbe :

normal[t_] := {y'[t], -x'[t]};
m[x_, y_] := x/4 + y - 1;
n[x_, y_] := 0.5 (x + y^2);
v[x_, y_] := {m[x, y], n[x, y]};
x[t_] := 5*Cos[t];
y[t_] := 3*Sin[t];
tmin = 0; tmax = 2Pi; ?t = Pi/10;
orig = Table[{x[t], y[t]}, {t, tmin, tmax, ?t}];
comp = Flatten[Table[{(v[x[t], y[t]].normal[t])/(Sqrt[
    normal[t].normal[t]])*normal[t]}, {t, tmin, tmax, ?t}], 1];
champ = {Hue[2/3], MapThread[Arrow, {orig, 
    orig + comp, Table[HeadScaling -> Relative, {Length[orig]}]}]};
courbe = ParametricPlot[{x[t], y[
    t]}, {t, tmin, tmax},
       PlotStyle -> {Hue[1/3], Thickness[0.005]}, 
                  DisplayFunction -> Identity];
perp = Show[courbe, Graphics[champ], Axes -> None, AspectRatio -> Automatic, 
          PlotRange -> All, DisplayFunction -> $DisplayFunction];

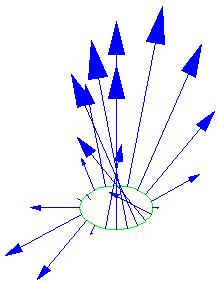
Nous avons donc ici le schéma du flux qui se révèle être un flux "sortant".

Pour calculer maintenant la valeur du flux, nous avons plus qu’à calculer l’intégrale de la composante normale :

NIntegrate[v[x[t], y[t]].normal[t], {t, tmin, tmax}]

Conclusion

La notion de flux est utilisé dans de nombreux domaines... que ce soit dans la physique (les exemples présentés ci-dessus, mais pas seulement !), la médecine (par exemple les flux de chaleur), dans la météorologie (le flux anémométrique entre autres), dans l’économie, ou encore dans la démographie (flux d’immigrants, d’émigrants etc), la notion et le fonctionnement de base sont les mêmes. Le flux est un mot fréquemment utilisé dans le langage courant, et souvent associé à la seule notion de débit par méconnaissance du sujet... Cependant, cette notion est loin d’être aussi restreinte qu’elle n’y paraît !