Exercices sur l’énergie et la quantité de mouvement relativistes.
par Bernard Vuilleumier
- a) Quelle énergie faut-il pour accélérer un électron de 0.57 c à 0.86 c ?
- b) Et pour accélérer un électron de 0.86 c à 0.99 c ?
Rép. 0.379 MeV, 2.621 MeV.
Exercice 2
Un proton se déplace à la vitesse 0.987 c.
- a) Que vaut son énergie de masse ?
- b) Que vaut son énergie totale ?
- c) Que vaut son énergie cinétique ?
Rép. 938 MeV, 5836 MeV, 4898 MeV.
Exercice 3
Une particule instable de masse 
kg se désintègre en deux fragments qui s’éloignent respectivement aux vitesses -0.772 c et 0.983 c. Que valent les masses de ces fragments ?
Rép. 
kg, 
kg.
Exercice 4
L’énergie cinétique d’un proton dans un accélérateur vaut 100 GeV.
- a) Que vaut sa vitesse ?
- b) Que vaut sa quantité de mouvement ?
Rép. 
m/s, 
kg m/s.
Exercice 5
Des électrons sont accélérés à une énergie de 15 GeV dans le SLAC (Stanford Linear Accelerator) qui mesure 3 km de long.
- a) Que vaut le facteur
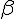pour ces électrons ? - b) Quelle est leur vitesse ?
- c) Que vaudrait la longueur de l’accélérateur s’il était observé depuis un référentiel lié à ces électrons (une fois qu’ils ont atteint cette vitesse).
Rép. 
, 
m/s, 
cm.
Exercice 6
Une particule instable de masse 
260 
se désintègre en un muon 
de masse 
= 206 et un antineutrino 
de masse 
. Que valent les énergies cinétiques du muon et de l’antineutrino ?
Rép. 2.866 MeV, 24.729 MeV.
Autres exercices
sur le calcul d’erreur
sur le mouvement
sur les mouvements relatifs
sur la relativité galiléenne
sur la relativité restreinte
sur les forces d’inertie
sur la quantité de mouvement
sur la gravitation
sur l’énergie
sur les oscillations harmoniques
sur l’énergie et les oscillations
sur la rotation de solides rigides
sur la notion de flux
sur les grandeurs de l’électromagnétisme et leurs relations
sur le mouvement de particules chargées dans un champ électrique
sur l’induction et l’auto-induction