Exercices extraits de J. Cessac, G. Tréherne, Physique, classe terminale C. Fernand Nathan, Paris 1967.

Exercice 1
Un treuil est constitué d’un cylindre homogène de masse M=20 kg, de rayon r=10 cm et d’axe Z. Une corde enroulée sur le treuil soutient un solide S de masse m=10 kg. Les masses de la corde et de la manivelle ainsi que toutes les résistances passives (frottements et résistance de l’air) sont négligeables. Calculez :

1. la tension T de la corde en situation d’équilibre ou de rotation uniforme
2. l’accélération angulaire 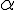du treuil si on lâche la manivelle
3. l’accélération linéaire a du solide S dans sa chute lorsqu’on lâche la manivelle.

– Rép. 98.1 N, 49.05 rad/s², 4.905 m/s².

Exercice 2
Un petit gyroscope cylindrique de masse m=100 g et de 5 cm de rayon tourne autour de son axe à raison de 3600 tours par minute. Sachant qu’il s’arrête en 3 minutes sous l’action de résistances passives équivalentes à un couple que vous supposerez constant, calculez :

1. l’accélération angulaire 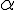du gyroscope
2. le moment 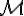du couple résistant
3. le nombre de tours n effectués entre le début du ralentissement et l’arrêt.

– Rép. rad/s², Nm,

Exercice 3
Un cylindre homogène de rayon r=10 cm et de masse =1 kg peut tourner autour de son axe de révolution horizontal Z. Il soutient un solide S de masse M=10 kg par l’intermédiaire d’une corde enroulée sur le cylindre. Le cylindre est traversé, suivant un diamètre, par une tige t portant à ses extrémités deux masses égales de valeur m=0.5 kg, pratiquement confondues avec leurs centres de gravité situés à une distance l=50 cm de l’axe Z. Le système est abandonné à lui-même sans
vitesse initiale. Calculez, en négligeant les masses de la corde et de la tige t ainsi que les résistances passives :

1. l’accélération linéaire a du mouvement de S
2. la tension T du brin qui supporte S pendant ce mouvement
3. le nombre de tours n effectués par le cylindre depuis le départ jusqu’au moment où la corde quitte le cylindre sachant que la masse M est alors descendue d’une hauteur h=5 m
4. la vitesse angulaire 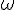du cylindre à ce moment là.

– Rép. 2.76 m/s², 70.47 N, 7.96, 52.57 rad/s.

Exercice 4
Un fil de masse négligeable passe sur la gorge d’une poulie de 100 g et de rayon r=6 cm. Vous supposerez que la poulie tourne sans frottement autour d’un axe horizontal et que toute la masse de la poulie est répartie sur sa circonférence. Le fil porte une masse M=300 g et une masse m=100 g. La masse M se trouve à 3 m au-dessus du sol et la masse m est au niveau du sol sans toutefois y reposer. Vous abandonnez le système à lui-même au temps t=0. Calculez :

1. l’accélération prise par la masse M
2. la tension T dans chaque brin pendant le mouvement
3. la vitesse v de M lorsqu’elle arrive au sol
4. la vitesse angulaire 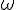de la poulie lorsque M arrive au sol
5. la force tangentielle F qu’il faut appliquer à la poulie pour qu’elle s’arrête après 6 tours, le fil supportant m étant coupé quand M arrive au sol.

– Rép. 3.92 m/s², 1.77 et 1.37 N, 4.85 m/s, 80.87 rad/s, 0.52 N.

Exercice 5
Le pendule à ressort spiral qui règle le mouvement d’une montre a un moment d’inertie par rapport à l’axe de rotation de et une période de 0.5 s. Calculez :

1. la constante C du couple de rappel ;
2. la vitesse angulaire 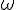maximale quand l’amplitude vaut 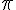radians
3. le moment du couple de rappel quand l’amplitude vaut

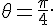
– Rép. Nm, rad/s, Nm.

Autres exercices
– sur le calcul d’erreur
– sur le mouvement
– sur les mouvements relatifs
– sur la relativité galiléenne
– sur la relativité restreinte
– sur les forces d’inertie
– sur la quantité de mouvement
– sur la gravitation
– sur l’énergie
– sur l’énergie relativiste
– sur les oscillations harmoniques
– sur l’énergie et les oscillations
– sur la notion de flux
– sur les grandeurs de l’électromagnétisme et leurs relations
– sur le mouvement de particules chargées dans un champ électrique
– sur l’induction et l’auto-induction