Épreuve d'applications des maths - [S'informer et apprendre en ligne]

Mardi 18 mars

Épreuve d’applications des maths

Épreuve d’applications des maths. Travail d’élève.

Article mis en ligne le 1er avril 2008

dernière modification le 17 août 2008

par Aymeric Genet

Problème 1

a) L’équation différentielle générale permettant d’obtenir les graphiques demandés est la suivante :

$y’(t) = c \cdot y(t) (y_{max}-y(t))$

Les valeurs que nous pouvons d’ores et déjà déterminer sont les suivantes :

Données	Valeurs
y₀	0.1
y_max	1

C’est le paramètre "c" qui changera la courbure des 4 courbes demandées.

b) Elle peut se résoudre à l’aide de Mathematica, de la manière suivante :

DSolve[y'[x] == c*y[x]*(1-y[x]),y[x],x]

y[x] = E^(c x)/(9 + E^(c x))

c) Le paramètre c doit être égal aux valeurs suivantes afin d’obtenir les graphiques demandés :

Courbes	c
#1	0.4
#2	0.6
#3	0.8
#4	1.0

Ce paramètre est bien sûr estimé et possède une marge d’erreur de ± 0.05.

d) L’occupation d’une niche écologique pourrait être un exemple de ce modèle.

e) Dans cette condition, les données sont les suivantes :

Données	Signification
y(t)	Le nombres d’individus, ou la population en fonction du temps.
y’(t)	L’augmentation des naissances par unité de temps.
y₀	La population initiale lorsque t = 0.
y_max	La population maximale, ou la capacité du milieu.
c	Paramètre ou taux de croissance de la population.

Problème 2

a) L’équation peut s’écrire de manière différente afin d’être résolue plus facilement grâce à Mathematica :

$\frac{dy}{dx} = e^{-y} Cos^2(\pi x)$

$y’(x) = E^{-y} Cos^2(\pi x)$

Donc, elle peut être résolue de la manière suivante :

DSolve[y'[x] == e^(-y[x])*Cos[Pi * x]^2,y[x],x]

y[x] == Log[ C[1] + 1/2(x + Sin[2*Pi*x]/(2Pi))]

b) Sachant qu’en x = 0, y = ln(e), le graphique de la solution pour 0 < x < $\pi$ est le suivant :

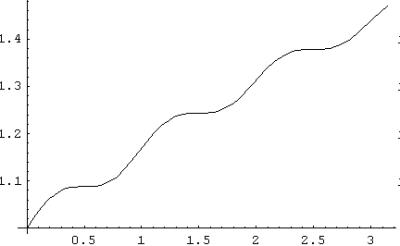
Problème 3

a) La solution de l’équation y’ = 2x² - y/x satisfaisant la condition initiale est la suivante :

DSolve[{y'[x] == 2x^2 - y[x]/x, y[1] == 3}, y[x], x]

y[x] = (5 + x^4)/2x

b) Le graphique de cette solution pour -4 < x < 4 est le suivant :

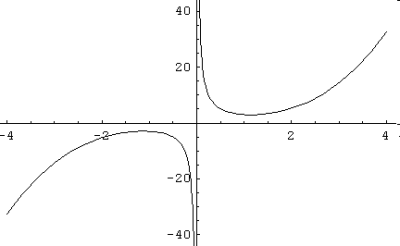
Problème 4

a) La solution générale de l’équation x’’ + x = 0 est la suivante :

DSolve[x''[t] + x[t] == 0, x[t], t]

x[t] = C[1] * Cos[t] + C[2] * Sin[t]

b) Pour déterminer les valeurs des constantes d’intégration sachant qu’en t = 0, x = 1 et x’[t] = 2, il faut poser les conditions dans Mathematica de la manière suivante :

DSolve[{x''[t] + x[t] == 0, x[0] == 1, x'[0] == 2}, x[t], t]

x[t] = Cos[t] + 2 Sin[t]

c) Le graphique de cette solution satisfaisant les conditions pour t variant de 0 à $2\pi$ est le suivant :

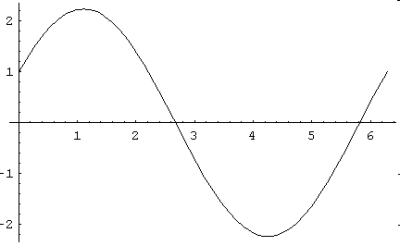
d) Pour obtenir la solution correspondant aux valeurs aux limites x(0) = 1 et $x(\frac{\pi}{2}) = 0$ , il faut poser les conditions et résoudre l’équation avec Mathematica, puis dessiner la fonction, de la manière suivante :

DSolve[{x''[t] + x[t] == 0, x[0] == 1, x[Pi/2] == 0}, x[t], t]

x[t] = Cos[t]

Plot[Cos[t],{t,0,2Pi}]

Ce qui nous donne le graphique suivant :

Problème 5

a) Pour résoudre numériquement le système d’équations :

$x’(t) = 1 + x(t)²y(t) - \frac{7}{2} \cdot x(t)$
$y’(t) = \frac{5}{2} \cdot x(t) - x(t)²y(t)$

Il faut savoir que pour résoudre numériquement une équation, il faut déterminer une portée pour t, allant d’un t_min à un t_max. Nous allons donc déterminer t_min = 0, et t_max = 10, répondant ainsi directement au deuxième point, et utiliser la formule NDsolve dans Mathematica de la manière suivante :

NDSolve[{x'[t] == 1+x[t]^2*y[t]-7/2*x[t],y'[t] == 5/2*x[t]-x[t]^2*y[t],x[0] == 0,y[0] == 0},{y[t],x[t]},{t,0,1}]

b) Le graphique obtenu de ce système d’équations, avec t variant de 0 à 10, est le suivant :

c) Pour x(0) variant de 0 à 3, il faut lancer dans Mathematica le code suivant :

sol=Table[NDSolve[{x'[t] == 1+x[t]^2*y[t]-7/2*x[t],y'[t] == 5/2*x[t]-x[t]^2*y[t],x[0] == x0,y[0] == 0},{y[t],x[t]},{t,0,1}],{x0,0,3}];

Table[Plot[sol[[x0, 1, 1, 2]], {t, 0, 1}],{x0,1,4}];

Table[Plot[sol[[x0, 1, 2, 2]], {t, 0, 1}], {x0, 1, 4}];

Les quatre premiers graphiques sont les graphiques de x(t), les quatre suivants sont les graphiques pour y(t).