Épreuve semestrielle de physique 1e année

Forces, mouvement, énergie mécanique

Article mis en ligne le 19 juin 2006

dernière modification le 28 août 2011

par Marti Ruiz-Altaba

Voici le corrigé de l’épreuve regroupée de physique de première année (niveau 1) qui a eu lieu le 9 juin 2006 au Collège Nicolas Bouvier (Genève). Vous trouvez en pièces jointes l’énoncé et aussi le corrigé détaillé.

L’épreuve, difficile, avait quatre questions :

Vrai ou faux ? (16 pts)
Puck sur glace (15 pts)
Cyclisme Genève-Versoix et retour (16 pts)
Luge (16 pts)

Les énoncés sont en cursive, les réponses en lettre normale.

Vrai ou faux ? (16 pts)

Répondez par vrai (V) ou faux (F) aux affirmations suivantes, en justifiant chacune de vos réponses.

– Un mobile accélère parce qu’il subit une force résultante non-nulle.

VRAI.

Si $\vec F$ est la force résultante sur l’objet de masse , et $\vec a$ est son accélération, alors depuis Newton on sait que

$\vec F = m \cdot \vec a$

Puisque $\vec a\ne0$ , alors forcément $\vec F\ne0$ .

– Une cycliste qui descend une pente à vitesse constante de 10 [km/h] ne subit aucune force.

FAUX.

Puisque sa vitesse est constante et la route est supposée sans virages, l’accélération de la cycliste est zéro. Donc, la force résultante sur la cycliste est zéro. Mais que l’addition de toutes les forces sur la cycliste soit zéro ne veut pas dire qu’elle ne subit aucune force ! Au moins, elle est attirée par la terre et tenue par le siège du vélo...

– Si l’on tire une charrette en ligne droite avec une force constante de 200 [N], cette charrette subit une acc’elération constante.

FAUX.

On a beau tirer avec une force constante, on ne sait pas si la force résultante sur la charrette est constante.

– Tout objet immobile subit une force résultante nulle.

VRAI.

La vitesse d’un objet immobile reste égale à zéro, donc son accélération est zéro, donc la force résultante sur lui est aussi zéro.

– Un ascenseur qui monte à la vitesse constante de 1 [m/s] subit une force résultante non-nulle.

FAUX.

S’il monte à vitesse constante, son accélération est nulle, et donc la force résultante sur lui est nulle.

– Tout corps en mouvement subit une force résultante non-nulle.

FAUX.

On peut très bien bouger à vitesse constante, sans accélérer, donc avec force résultante zéro.

– L’énergie totale est toujours conservée.

VRAI.

C’est l’énoncé le plus puissant et le plus universel découvert par les physiciennes et physiciens jusqu’ à aujourd’hui. On ne sait pas très bien ce qu’est l’énergie en général ou en abstrait, mais on sait très bien ce qu’elle est dans des cas concrets, et à chaque fois que l’on a mesuré l’énergie de quelque chose avant et après, l’énergie a toujours été la même.
Il n’y a aucune circonstance dans l’univers où l’énergie ne soit pas conservée.

– L’énergie mécanique est toujours conservée.

FAUX.

L’énergie mécanique est conservée tant qu’il n’y a pas de frottements, et tant qu’il n’y a pas d’apport d’énergie sous autres formes (énergie chimique dans vos muscles ou dans l’essence, énergie électrique, etc.)

Puck sur glace (15 pts)

Un joueur de hockey sur glace donne un coup de canne dans un puck de 150 [g], immobile sur la glace. Celui-ci part à toute vitesse en direction du gardien de but. Pendant l’impact qui dure un dixième de seconde, le puck subit de la part de la canne une force constante ainsi qu’une force de frottement constante dont l’intensité vaut 1,5 [N]. Au moment où la canne cesse d’agir sur le puck, sa vitesse est de 72 [km/h].
– Sur la figure ci-dessous, représentez, en les nommant, toutes les forces qui s’exercent sur le puck pendant l’impact. (4 pts)

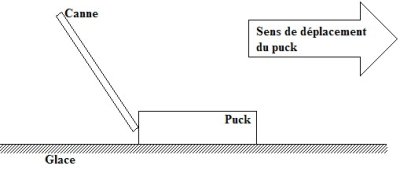
– Calculez l’intensité de la force exercée par la canne sur le puck pendant l’impact. (7 pts)
Le puck glisse ensuite sur la glace de la patinoire, en subissant la même force de frottement que pendant l’impact.
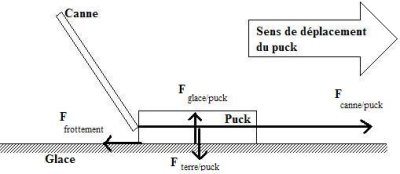
– Sur la figure ci-dessous, représentez, en les nommant, toutes les forces qui s’exercent sur le puck après l’impact. (1 pt)

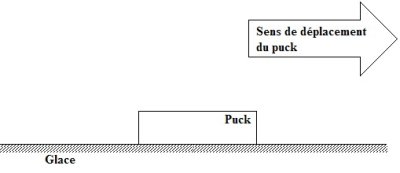
– Quelle accélération le puck subit-il alors ?(3 pts)
– BONUS : Quelle distance le puck parcourt-il sur la glace avant de s’immobiliser ? (6 pts)

– Il y a quatre forces qui agissent sur le puck pendant l’impact :

la force d’attraction gravitationnelle de la terre sur le puck $\vec F_{\rm terre/puck}$ qui agit au centre du puck vers le bas ;
la force de la glace sur le puck 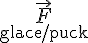$\vec F_{\rm glace/puck}$ qui agit sur la surface inférieure du puck, vers le haut ;
la force de la canne sur le puck 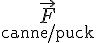$\vec F_{\rm canne/puck}$ qui agit sur le point de contact entre le puck et la canne ; cette force est supposée horizontale ;
la force de frottement $\vec F_{\rm frottement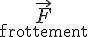}$ qui agit en sens opposé au mouvement (donc horizontalement vers la gauche) sur la surface entre le puck et la glace ; c’est en effet une autre force de la glace sur le puck.

Nous savons que les deux forces verticales ont la même longueur, et que la force de la canne sur le puck est beaucoup plus grande que la force de frottement (autrement le puck ne partirait pas). Leurs longueurs précises, avec échelle, ne peuvent être connues qu’après calculs.

– Il nous faut d’abord trouver la force résultante sur le puck pendant l’impact. Il nous faut donc calculer en premier l’accélération du puck.

La vitesse initiale du puck est , tandis que la vitesse finale est

$v=72 \rm[km/h] = 72 \left[\frac{km}{h}\right] \cdot \frac{10^3 [m]}{1 [km]}\cdot\frac{1 [h]}{60\cdot 60 [s]} = 20 [m/s]$

Il faut un dixième de seconde pour passer de la vitesse initiale à la vitesse finale , donc l’accélération moyenne pendant ce dixième de seconde vaut

$a=\frac{\Delta v}{\Delta t} = \rm\frac{20 [m/s]-0 [m/s]}{0,1 [s]}=2\cdot 10^2 [m/s^2]$

$\vec F _{\rm r\acute{e}sultante}=m\cdot \vec a \Rightarrow F_{\rm r\acute{e}sultante} =\rm 0,150 [kg]\cdot 2\cdot 10^2 [m/s^2] = 3\cdot 10^1 [N]$

On a supposé que la canne n’exerce pas de force verticale sur le puck. C’est à dire, que la force de la canne sur le puck est horizontale. Mais d’après le diagramme, il est clair que la force résultante est aussi horizontale, telle que

$\vec F _{\rm r\acute{e}sultante}= \vec F_{\rm canne}- \vec F _{\rm frottement}$

comme quoi l’intensité de $\vec F_{\rm canne}$ est

$F_{\rm canne}= \rm 3\cdot 10^1 [N] + 1,5 [N] = 3 \cdot 10^1 [N]$

La durée de l’impact est connue avec un seul chiffre significatif, comme quoi la force de frottement est négligeable pendant l’impact.

– C’est les mêmes forces que sur le dessin précédent, excepté la force de la canne sur le puck. Même si le puck avance vers la droite, la force résultante sur lui est vers la gauche (c’est pour cela qu’il va s’arrêter).

– Les deux forces verticales sur le puck (attraction gravitationnelle de la terre et soutien de la glace) s’annulent, et la force résultante est égale à la force de frottement, qui vaut 1,5 [N] mais en sens opposé au mouvement :

$a= \frac{-F}{m}=\rm \frac{-1,5 [N]}{0,150 [kg} =- 10 [m/s^2]$

– On compte les distances et les temps à partir du moment où le puck ne touche plus la canne, c’est à dire après le dixième de seconde de contact entre le puck et la canne. Dès ce moment, le puck ne subit plus que l’accélération calculée ci-dessus. Il commence son mouvement avec la vitesse $v_0=\rm72 [km/h]=20 [m/s]$ et le finit avec une vitesse nulle, $v=0 \rm [m/s]$ . Nous voulons calculer la distance parcourue

. Les formules requises sont

$v(t)=v= v_0 + a\cdot t$

$s(t)=s= s_0 + v_0\cdot t + \frac12 a \cdot t^2$

Tel que nous avons choisi de mesurer la distance, $s_0=0 \rm[m]$ .
De la première équation nous sortons

, et ensuite nous employons la deuxième pour calculer

$v= v_0 + a\cdot t \Rightarrow t = \frac{v-v_0}{a} = \rm \frac{0-20 [m/s]}{-10 [m/s^2]} =2,0 [s]$

$s= s(2,0 \rm [s]) = 20 [m/s]\cdot 2,0 [s] + \frac12 (-10 [m/s^2]) \cdot (2,0 [s])^2 = 20 [m]$

Le puck voyage donc pendant 2,0 [s] avant de s’arêter 20 [m] plus loin. Le frottement est très fort : la glace de la patinoire est très usée.

Cyclisme Genève-Versoix et retour (16 pts)

Andréa et sa maman ont décidé d’aller faire un tour à vélo. Elles ont choisi de partir de Genève, d’aller à Versoix puis de revenir à leur point de départ. Genève et Versoix sont distants de 15 [km].
Andréa est sportive et part à midi à la vitesse de 25 [km/h], qu’elle maintient jusqu’ à Versoix. Elle revient à Genève à vitesse constante mais plus lentement, de sorte que sa vitesse moyenne sur le trajet complet est de 20 [km/h].
La maman, qui est partie 20 [min] après Andréa, commence à être \^agée. Elle parcourt le trajet complet sans empressement, à la vitesse constante de 10 [km/h].

– Représentez graphiquement les positions des deux cyclistes en fonction du temps pour le trajet complet. (8 pts)
Remarque : Choisissez les échelles de sorte à occuper le maximum de place disponible sur le graphique.

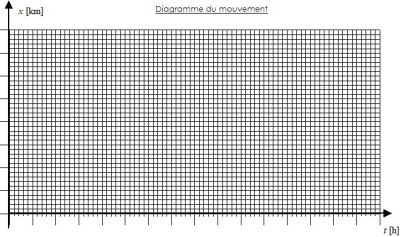
Il est important de se convaincre que le graphiques de chaque cycliste est un volcan'': une droite qui monte ($x$ augmente à mesure que $t$ augmente) suivie d'une droite qui descend ($x$ diminue quand $t$ continue d'augmenter). La variable $x$ représente la distance depuis Genève; ainsi un zig-zag qui monte et redescend s'interprète comme un aller-retour. Plaçons Genève à l'origine des $x$. Il est commode de compter 2~[km] pour chaque grosse division, pour finir avec Versoix presque au bord du graphique. Plaçons midi (12~[h]) à l'origine du temps. La maman est lente et doit parcourir 30~[km] à 10~[km/h], ce qui lui prendra trois heures (plus les vingt minutes de retard initial). Il est commode de choisir une heure égale à quatre grosses divisions, comme quoi une division est un quart d'heure et l'intervalle entre deux traits fins consécutifs est de trois minutes. <img1228|center> La maman partira donc à 13h20 et reviendra à 16h20, et pile entre les deux (à 14h50) elle sera à Versoix. Nous traçons les deux traits comme dans le dessin. La fille part à 12h00 avec une vitesse de 25~[km/h], comme quoi nous pla\c cons le point $\rm (12h30;12,5~[km])$ et tirons la droite le reliant à l'origine. Nous ne retenons de cette droite que le morceau entre $x=0\rm~[km]$ et $x=15\rm~[km]$. Comme Andréa roule à une vitesse moyenne de 20~[km/h], en tout il lui faut $\rm \frac {30~[km]}{20~[km/h]} = 1,5~[h]$, comme quoi elle revient à 13h30. Nous pla\c cons donc le point (13h30;0~[km]) et le relions au point où la droite aller d'Andréa atteint les 15~[km]. - {Sur votre graphique, entourez le point représentant la rencontre des deux cyclistes puis donnez-en l'heure et le lieu. (3~pts)} Elles se croisent à 13 heures et quatre minutes, à 7,4~[km] de Genève. Il faut prendre la précision de ce résultat avec pincettes. - {Où se trouve la maman quand Andréa fait demi-tour ? (1 pt)} Elle se trouve à 2,8~[km] de Genève. - {Posez les équations qui permettent de déterminer algébriquement où et quand a lieu la rencontre. Choisissez, pour ce faire, $t = 0 ~\rm[h]$ au moment où Andréa commence à rentrer. (4~pts)} Andréa commence à rentrer après avoir atteint Versoix, donc après $$ \rm \frac {15~[km]}{25~[km/h]} = 0,60~[h]$$ à ce moment, elle se trouve à $x=x(0) =x_0 = 15~\rm [km]$. Lorsqu'Andréa commence à rentrer, donc à $t=0$, la maman a déj à roulé pendant $$0,60~[\rm h]- 0,33~[h]= 0,27~[h]$$ et sa vitesse est toujours de 10~[km/h]. Elle a donc déj à parcouru une distance de $$0,27\rm~[h]\cdot 10~[km/h]= 2,7~[km]$$ ce qui est proche du résultat graphique. L'équation de sa trajectoire est donc $$x_M(t) = {\rm 2,7~[km]+10~[km/h]}\cdot t $$ Andréa se trouve à 15~[km] de Genève et rentre, donc sa vitesse sera négative. Pour trouver la valeur de sa vitesse, pourtant, il faut encore la calculer. Nous savons que la vitesse à l'aller était de 25~[km/h] et en tout de 20~[km/h]. Pour trouver la vitesse au retour, il faut égaliser les temps: $$\textrm{temps aller + temps retour}= \rm \frac{30~[km]}{20~[km/h]} = 1,5~[h]$$ $$\textrm{temps aller}= \rm \frac{15~[km]}{25~[km/h]} = 0,60~[h]$$ $$\textrm{temps retour}= {\rm 1,5~[h]-0,60~[h] = 0,9~[h] }= \frac{15~\rm [km]}{v} $$ et donc $$ v = \rm \frac{15~[km]}{0,9~[h]}= 2\cdot 10^1 ~[km/h]$$ et non pas $17~\rm [km/h]$ parce que nous n'avons pas assez de chiffres significatifs. L'équation de la trajectoire d'Andréa au retour est donc $$x_A(t) = {\rm 15~[km]- 2\cdot 10~[km/h]}\cdot t$$ - {BONUS : Résolvez ces équations. (5~pts)} $$\left. \matrix{ x_A(t) &=& {\rm 15~[km]- 2\cdot 10~[km/h]}\cdot t\cr x_M(t) &=& {\rm 2,7~[km]+10~[km/h]}\cdot t \cr}\right\}$$ La condition algébrique de la rencontre est $x_A=x_M$. En travaillant sur $x_A(t)-x_M(t)$ nous pouvons trouver le $t$ auquel a lieu la rencontre: $${\rm 15~[km]- 2\cdot 10~[km/h]}\cdot t = {\rm 2,7~[km]+10~[km/h]}\cdot t $$ $${\rm 15~[km]- 2,7~[km]} = {\rm 2\cdot 10~[km/h]}\cdot t+{\rm 10~[km/h]}\cdot t $$ $${\rm 12~[km]} = {\rm 3\cdot 10~[km/h]}\cdot t $$ $$t=\rm0,4~[h]$$ ce qui veut dire 24 minutes plus ou moins 0,1~[h]=6 minutes. D'après la montre, elles se croisent à $$\rm 12h00+0,27~[h]+0,4~[h]= 12,7~[h]= 12h42min \pm 6 ~min$$ Maintenant nous pouvons calculer où se trouvent Andréa et sa maman à $t=0,4~\rm[h]$, et vérifier que la réponse est juste: $$ \matrix{ x_A({\rm 0,4~[h]}) &=& \rm 15~[km]- 2\cdot 10~[km/h]\cdot 0,4~[h] &=& \rm7~[km]\cr x_M({\rm 0,4~[h]}) &=& \rm 2,7~[km]+10~[km/h]\cdot 0,4~[h] &=& \rm 7~[km]\cr}$$ Le calcul algébrique est moins précis que le graphique (parce que nous n'avons pas inclus les incertitudes dans le graphique, où nous avons tracé les trajectoires comme des droites et non pas comme des familles de droites, ou des droitesépaisses’’).

Luge (16 pts)

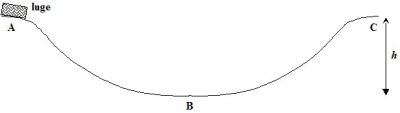
Une luge et son chargement ont une masse de 316,4 [kg] et glissent sans frottement sur la piste verglacée esquissée ci-dessus. Les positions A et C se trouvent à la même hauteur $h = 68,3 \rm[m]$ au-dessus de la position B. à l’instant $t = 0 \rm [s]$ , la luge se trouve en A avec une vitesse initiale .
– Si $v_0= 0 \rm [m/s]$ , à quelle vitesse la luge arrive-t-elle en C ? (2 pts)

Comme il n’y a pas de frottement, l’énergie mécanique est conservée.

Comme C se trouve à la même hauteur que A, l’énergie potentielle de la luge en C est égale à l’énergie potentielle de la luge en A. Donc forcément l’énergie cinétique de la luge en C est égale à l’énergie cinétique de la luge en A. Donc forcément la vitesse en C est égale à la vitesse en A, $0 \rm[m/s]$ .

– Si $v_0= 0 \rm [m/s]$ , à quelle vitesse la luge arrive-t-elle en B ? (6 pts)

Comme il n’y a pas de frottement, l’énergie mécanique est conservée.

Si nous mesurons les hauteurs à partir de B, la hauteur de B est zéro et donc l’énergie potentielle de la luge en B est zéro.

L’énergie potentielle de la luge en A est , avec $h=68,3 \rm[m]$ , $g=9,81 \rm [N/kg]$ et $m=\rm 316,4 [kg]$ .

L’énergie cinétique de la luge en A est zéro, puisque sa vitesse est zéro.

L’énergie cinétique de la luge en B est $\frac12 mv^2$ , avec justement inconnue et la masse de la luge.

Par conservation de l’énergie mécanique,

$E_{\rm potentielle}^A +E_{\rm cin\acute{e}tique}^A = E_{\rm potentielle}^B +E_{\rm cin\acute{e}tique}^B$

$m\cdot g\cdot h +0 = 0 + \frac12 m v^2$

En fait, la vitesse de la luge en B est indépendante de sa masse :

$mgh=\frac12mv^2 \Rightarrow v^2 = 2gh \Rightarrow v=+\sqrt{2gh}= 36,6 \rm [m/s]$

– Si $v_0 = 5,4 \rm[m/s]$ , à quelle vitesse la luge arrive-t-elle en C ? (2 pts)

Comme il n’y a pas de frottement, l’énergie mécanique est conservée.

– Si $v_0 = 5,4 \rm [m/s]$ , à quelle vitesse la luge arrive-t-elle en B ? (6 pts)

Comme il n’y a pas de frottement, l’énergie mécanique est conservée.

Si nous mesurons les hauteurs à partir de B, la hauteur de B est zéro et donc l’énergie potentielle de la luge en B est zéro.

L’énergie potentielle de la luge en A est , avec $h=63 \rm[m]$ , $g=9,81 \rm [N/kg]$ et la masse de la luge.

L’énergie cinétique de la luge en A est $\frac12 mv_0^2$ , avec $v_0=5,4 \rm[m/s]$ la vitesse initiale de la luge.

L’énergie cinétique de la luge en B est $\frac12 mv^2$ , avec justement inconnue.

Par conservation de l’énergie mécanique,

$E_{\rm potentielle}^A +E_{\rm cin\acute{e}tique}^A = E_{\rm potentielle}^B +E_{\rm cin\acute{e}tique}^B$

$m\cdot g\cdot h +\frac12 m v_0^2 = 0 + \frac12 m v^2$

En fait, la vitesse de la luge en B est indépendante de sa masse :

$mgh+\frac12mv_0^2=\frac12mv^2 \Rightarrow v^2 = v_0^2 +2gh \Rightarrow v=+\sqrt{2gh+v_0^2}= 37 \rm [m/s]$

Comme la vitesse initiale n’a que deux chiffres significatifs, la vitesse finale ne peut être calculée avec plus de précision. Notez que, à deux ciffres significatifs, c’est la même vitesse que quand la luge était partie du repos.

CORRIGé épreuve Semestrielle juin 2006 G1.PY1 Bouvier

Vrai ou faux ? (16 pts)

Puck sur glace (15 pts)

Cyclisme Genève-Versoix et retour (16 pts)

Luge (16 pts)

Dans la même rubrique