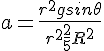Rotation d’une bille sur un rail

Accélération de la bille en fonction de son moment d’inertie

samedi 25 janvier 2014, par Bernard Vuilleumier

Théorie

Une bille roulant sur un rail incliné subit trois forces : son poids $m\vec g$ , une force de frottement $\vec F$ et une force de soutien $\vec N$ normale au plan. En projetant ces forces sur un axe parallèle au plan et en faisant usage de la relation fondamentale de la dynamique :

$\Sigma\vec F=m\vec a$

on obtient la grandeur de l’accélération du centre de masse (équation 1) :

$a=gsin\theta-\frac{F}{m}$

L’accélération angulaire $\alpha=\frac{a}{r}$ de la bille s’obtient à partir de la relation fondamentale de la dynamique appliquée aux corps solides en rotation :

$\Sigma M=I\alpha$

où $\Sigma M$ est la somme des moments de force qui agissent sur la bille et le moment d’inertie de la bille. La seule force dont le moment n’est pas nul est $\vec F.$ La relation ci-dessus s’écrit donc (équation 2) :

$Fr=I\alpha$

En éliminant la force de frottement entre l’équation 1 et l’équation 2, on peut exprimer l’accélération a de la bille en fonction de son rayon r, de son moment d’inertie I, de l’accélération du lieu g et de l’angle d’inclinaison θ du rail :

$a=\frac{mr^2gsin\theta}{mr^2+I}$

Cette expression se simplifie par m. L’accélération de la bille ne dépend pas de sa masse.

$a=\frac{r^2gsin\theta}{r^2+\frac{2}{5}R^2}$