A la suite de notre visite à la station Airbus puis à la cité de l’espace, certains sujets de travail nous on été proposés dont un qui traitait des satellites. Les satellites sont "omniprésents", il m’a donc paru intéressant de plus s’y intéresser. Voilà pourquoi j’ai choisi ce sujet.

Expliquez les notions de satellite à défilement et de satellite géostationnaire. À quels usages ces deux types de satellites sont-ils destinés ? Calculez la période de révolution de chacun de ces types de satellites.

Les Satellites

Les satellites artificiels sont des engins créés et placés dans l’espace par l’homme et qui sont placés en orbite autour de la Terre. Ils nous permettent principalement d’observer et de télé-communiquer. On distingue deux principaux "groupes" de satellites : les satellites géostationnaires et les satellites à défilement.

Principe d’un satellite géostationnaire

Le principe de ce satellite est de se trouver sur une orbite géostationnaire.

Sur ce schéma, la boule bleue est la terre. Le satellite est représenté en vert et nous avons le point de vision du satellite en marron.

Les satellites apparaissent donc comme immobiles au-dessus d’un certain point de la Terre. Ce qui veut dire que la vitesse angulaire du satellite est égale à celle de la rotation de la Terre et qu’il décrit une orbite circulaire dans un plan équatorial. Ce qui veut dire qu’une certaine partie de la terre est observée chaque jour à la même heure par un de ces satellites. Les satellites géostationnaires sont le plus souvent utilisés pour la météorologie, les télécommunications et la télévision directe.
Il faut aussi savoir que les satellites géostationnaires sont à une altitude de 36’000 km.

Principe d’un satellite à défilement

Les satellites à défilement contrairement aux satellites géostationnaires ne sont pas immobiles par rapport à un point fixe de la terre (ils défilent). Leurs vitesses est d’environ 7 km/s au-dessus de la surface terrestre. Ces satellites sont en orbite basse et défilent rapidement (environ 1h20 - 1h40 pour faire le tour de la Terre). Ils sont généralement utilisés en radioamateur et en constellations de téléphonie mobile.

Calcul de la période de révolution

Pour calculer la période de révolution d’un satellite à défilement, je vais dans un premier temps me servir de la 3ème loi de Kepler. Puis, dans un second temps, j’utiliserai la seconde loi de Newton. Pour faire tout cela, nous aurons besoin des données qui suivent :

– , la constante de la gravitation
– , le demi grand axe de la trajectoire elliptique
– , le rayon de la Terre
– , la distance entre la surface terrestre et le satellite
– 

Calcul d’après la 3ème loi de Kepler

Toutes les données sont connues, il nous suffit juste de remplacer par les valeurs. Cela nous donne :

Ce qui nous donne environ 1 heure et demi (1:33).

Calcul d’après la seconde loi de Newton

Il faut pour cette étape, égaler la force de gravitation à une force centripète. Ce qui donne :

En simplifiant et en substituant par on a :

Il nous reste plus qu’à isoler .

Enfin, il ne nous reste plus qu’à remplacer par les données connues.

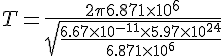
Nous obtenons le même résultat qu’au calcul précédent soit environ 1 heure et demi.

Pour un satellite géostationnaire, il faudrait remplacer les 500 km par 36’000 km. Nous savons dores et déjà que la période trouvée sera de 24h.

Sources :
– Le Petit Larousse ed. 2001
– www.wikipédia.org
– Table CRM