Le but de cette expérience est de déterminer l’accélération et le moment d’inertie de deux cylindres, l’un en aluminium (plein) et l’autre en laiton (évidé), sur un plan incliné.
par Florian Matthey, Jean-Pierre Trang
Lorsqu’on fait rouler un cylindre en aluminium plein et un cylindre en laiton évidé sur un plan incliné, on remarque qu’il y en a un qui arrive en bas avant l’autre. Cela veut dire que l’accélération subie par chacun des deux cylindres est différente. Pourtant, ils ont les mêmes dimensions : masses, longueurs, diamètre. Cette étrange différence est due au fait que la matière n’est pas répartie de la même façon autour de l’axe de rotation des cylindres, étant donné que l’un des deux est plein et l’autre évidé. La résistance d’un corps soumis à une mise en rotation est mesurée par le moment d’inertie.
Situation
Nous avons deux cylindres de même masse et de mêmes dimensions, l’un est plein et l’autre évidé, que nous laissons rouler sur un plan incliné d’ angle 
. À l’aide de deux cellules photoélectriques disposées en haut et en bas, nous pouvons mesurer le temps nécessaire à chacun des deux cylindres pour aller d’en haut jusqu’en bas. Ainsi, nous auront la possibilité de déterminer l’accélération subie par ces cylindres. Ces essais doivent être effectués plusieurs fois pour différents angles. Cela nous permettra d’avoir l’accélération moyenne, une mesure plus sûre, des deux cylindres pour chaque angle et de déterminer leur moment d’inertie.
Trois forces agissent sur ces cylindres durant l’expérience :
– La force de pesanteur :
- F = mg
– La force de frottement
– La force de soutien
Mesures
– Les deux cylindres ont la même masse :
- 1062 grammes
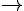1.062 kilogrammes.
– Le rayon et la masse des deux cylindres sont les mêmes, mais l’un des deux est évidé. À noter que les valeurs sont intégrées en centimètres.
- Dimensions des cylindres :
| Cylindre | rayon | rayon intérieur | longueur |
|---|---|---|---|
| Aluminium plein | 2.5 | - | 21 |
| Laiton évidé | 2.5 | 2.1 | 21 |
L’incertitude est de 
0.1 centimètre pour la longueur et le rayon. Elle est de 0.1 gramme, soit 0.0001 kilogramme pour la masse.
– La distance séparant les deux cellules photoélectriques et de 90 centimètres. L’incertitude est de 0.1 centimètre .
– Nous avons effectué l’expérience avec cinq inclinaisons différentes. Ci-dessous les temps effectués par les deux cylindres sur chaque inclinaison :
- Cylindre en aluminium :
| Pente | Temps moyen |
|---|---|
| 2.27° | 2.76 s |
| 3.36° | 2.11 s |
| 5.08° | 1.56 s |
| 7.11° | 1.33 s |
| 7.83° | 1.09 s |
- Cylindre en laiton :
| Pente | Temps moyen |
|---|---|
| 2.27° | 3.07 s |
| 3.36° | 2.31 s |
| 5.08° | 1.73 s |
| 7.11° | 1.48 s |
| 7.83° | 1.17 s |
Calculs et graphiques
Sachant que la masse volumique est définie par :
Il nous suffit de trouver le volume des cylindres pour déterminer leur masse volumique.
Le volume d’un cylindre est exprimé par :
Le volume du cylindre en aluminium est :
Et le volume du cylindre en laiton est le même sauf que nous devons lui soustraire le volume de la cavité :
Donc le volume du cylindre en laiton nous est donné par :
Maintenant nous pouvons déterminer la masse volumique des deux cylindres :
- Aluminium :
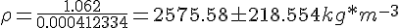
- Laiton :
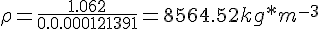
Leur masse volumique selon la table CRM sont respectivement de 2700 et 8470.
– Calcul de leur accélération :
Cylindre en laiton :
| Pente | Accélération |
|---|---|
| 2.27° | 0.094 m/s² |
| 3.36° | 0.17 m/s² |
| 5.08° | 0.30 m/s² |
| 7.11° | 0.41 m/s² |
| 7.83° | 0.68 m/s² |
Voici le graphique de son accélération en fonction du sinus de la pente :
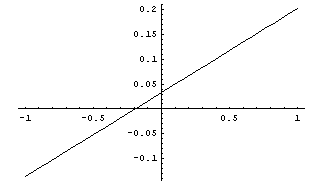
Cylindre en aluminium :
| Pente | Accélération |
|---|---|
| 2.27° | 0.12 m/s² |
| 3.36° | 0.20 m/s² |
| 5.08° | 0.37 m/s² |
| 7.11° | 0.51 m/s² |
| 7.83° | 0.76 m/s² |
Voici le graphique de son accélération en fonction du sinus de la pente :
En transformant la formule 
, nous obtenons cette formule pour le moment d’inertie :
Voici les résultats obtenus pour plusieurs accélérations en utilisant la formule ci-dessus, les moments d’inertie étant exprimés en 
:
Cylindre en aluminium :
| Pente | Accélération | Moment d’inertie |
|---|---|---|
| 2.27° | 0.12 m/s² | 0.001485475 |
| 5.08° | 0.37 m/s² | 0.000894524 |
| 7.11° | 0.51 m/s² | 0.000916534 |
Cylindre en laiton :
| Pente | Accélération | Moment d’inertie |
|---|---|---|
| 2.27° | 0.09 m/s² | 0.002079942 |
| 5.08° | 0.30 m/s² | 0.001258121 |
| 7.11° | 0.41 m/s² | 0.001301969 |
– Les tables CRM nous donnent cette formule pour le moment d’inertie d’un cylindre plein :
– Le moment d’inertie d’un cylindre évidé est :
- Le moment d’inertie du cylindre en aluminium est de 0.00033 .
- Le moment d’inertie du cylindre en laiton est de 0.00023 .
Synthèse :
On remarque que les valeurs obtenues expérimentalement ne sont pas les mêmes que celles avec la table CRM, cependant on constate qu’elles se rapprochent de plus en plus de ces chiffres lorsque l’angle d’inclinaison est plus élevé car l’accélération augmente.
Cette différence est principalement due à l’incertitude sur les mesures que nous avons effectuées, c’est pour cela que nous avons différentes valeurs qui se rapprochent néanmoins des valeurs de la formule dans la table CRM.
Conclusion :
Grâce à la durée de la descente, à l’accélération, à la masse, au rayon des cylindres, il est possible de calculer le moment d’inertie de celui-ci. Il faut en outre connaître l’inclinaison de la pente pour pouvoir utiliser cette formule.
Les incertitudes expliquent souvent les différences entre les valeurs théoriques et les valeurs pratiques, bien qu’il y ait aussi des éléments extérieurs qui rentrent en jeu. Ces calculs d’incertitude permettent d’avoir une vue plus précise sur la justesse des résultats.