– Champ : dynamique du solide rigide
– Documents autorisés : Tables numériques CRM. Calculette.
– Vendredi 16 mars 2007, CECNB, M3-M4, 95 min.
– Moyenne de classe : 4.47
– Écart type : 1.10
– Effectif : N=16

QCM

– Question 1 (2 points)

La relation fondamentale de la dynamique appliquée aux rotations :

• établit un lien entre une grandeur dynamique et une grandeur cinématique au même titre que .
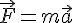• postule une proportionnalité entre moment de force et accélération angulaire
• postule une augmentation linéaire de l’accélération angulaire.

– Question 2 (4 points)

Le moment d’inertie d’un cylindre en rotation autour de son axe dépend :

• de la vitesse angulaire
• de l’accélération angulaire
• de la fréquence de rotation
• du rayon du cylindre
• de la longueur du cylindre.

– Question 3 (12 points)

Un treuil est constitué d’un cylindre homogène de masse M, de rayon r et d’axe Z. Une corde enroulée sur le treuil soutient un solide S de masse m. Les masses de la corde et de la manivelle ainsi que toutes les résistances passives (frottements et résistance de l’air) sont négligeables.

a) En situation d’équilibre :

• le moment d’inertie du cylindre est nul
• le moment d’inertie du cylindre est constant
• le moment de force exercé par la corde sur le cylindre est nul
• la tension de la corde est égale au poids du solide S
• la somme algébrique des moments par rapport à l’axe de rotation est nulle.

b) En rotation uniforme :

• le moment d’inertie du cylindre est constant
• le moment de force exercé par la corde sur le cylindre est constant
• la tension de la corde est égale au poids du solide S
• la tension de la corde est supérieure au poids du solide S si celui-ci s’élève
• la tension de la corde est inférieure au poids du solide S si celui-ci descend.

c) Lorsqu’on lâche la manivelle :

• le moment d’inertie du cylindre reste constant
• le moment d’inertie du cylindre augmente
• la somme algébrique des moments par rapport à l’axe de rotation reste constante
• la somme algébrique des moments par rapport à l’axe de rotation augmente
• la tension de la corde est inférieure au poids du solide S.

Question 4 (4 points)

Un petit gyroscope cylindrique de masse m et de rayon r tourne autour de son axe à une fréquence $\nu$. Sous l’effet d’un couple constant, il s’arrête en un temps t. Durant le ralentissement :

• l’accélération angulaire du gyroscope est constante
• l’accélération angulaire du gyroscope diminue
• la vitesse angulaire $\omega$ du gyroscope décroît linéairement
• le nombre de tours effectués jusqu’à l’arrêt vaut $\frac\omega t2$
• le nombre de tours effectués jusqu’à l’arrêt vaut $\nu t$.

Question 5 (4 points)

Un cylindre homogène de rayon r et de masse m peut tourner autour de son axe de révolution horizontal Z. Il soutient un solide S de masse M par l’intermédiaire d’une corde enroulée sur le cylindre. Le système est abandonnée à lui-même sans vitesse initiale. Si la masse de la corde ainsi que les résistances passives sont négligeables :

• l’accélération linéaire de S est constante
• l’accélération linéaire de S augmente
• l’accélération linéaire de S est proportionnelle à l’accélération angulaire
• la tension de la corde est proportionnelle à l’accélération angulaire.
• la tension de la corde est inversement proportionnelle à l’accélération angulaire

Question 6 (4 points)

Un fil de masse négligeable passe sur la gorge d’une poulie de masse m’ et de rayon r. La poulie tourne sans frottement autour d’un axe horizontal. Le fil porte une masse M à une extrémité et une masse m à l’autre (M > m). Vous abandonnez le système à lui-même :

• la tension n’est la même dans les deux brins que si m’ est négligeable.
• la tension est plus grande dans le brin qui supporte M que dans celui qui supporte m
• la tension est plus petite dans le brin qui supporte M que dans celui qui supporte m
• la tension est supérieure au poids de m dans le brin qui supporte m
• la tension est inférieure au poids de m dans le brin qui supporte m

Problème

Deux objets de masse m et M, avec M > m, sont attachés aux extrémités d’un fil. Celui-ci est enroulé sur une poulie d’axe horizontal et de masse négligeable. Initialement, les deux objets sont immobiles et leurs bases sont séparées par une distance h.

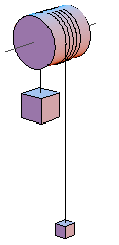
1. Exprimez la vitesse des objets lorsqu’ils se croisent (leurs bases se trouvent alors les deux à la même hauteur).
2. Que devient cette vitesse v si la masse de la poulie de rayon r n’est pas négligeable et si celle-ci possède un moment d’inertie $I=\fracm_poulier^22$ et une énergie cinétique de rotation $E_cin=\fracI\omega^22$ au moment où les masses se croisent ?
3. Calculez ces vitesses pour les valeurs suivantes : M=1 kg, m=200 g, h=1 m, r=5 cm et $m_poulie$=1 kg.

Corrigé

On obtient l’accélération a des masses en appliquant la relation fondamentale de la dynamique à chacune d’elles et à la poulie, puis en éliminant les tensions $T_1$ et $T_2$ entre ces trois équations. On trouve :

Avant de se croiser, les masses parcourent une distance h/2 en un temps . Leur vitesse vaut donc ;

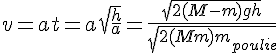
On peut aussi résoudre le problème en considérant l’énergie mécanique du système qui est la même en situation initiale et lorsque les masses se croisent. En fixant l’origine du système de référence à la hauteur de m et en égalant les énergies mécaniques, on obtient une équation qu’il faut alors résoudre par rapport à v pour obtenir la vitesse.

Réponses
– Sans tenir compte de la masse ou de l’énergie cinétique de rotation de la poulie, on obtient une vitesse v=2.56 m/s.
– En tenant compte de la masse ou de l’énergie cinétique de rotation de la poulie, on obtient une vitesse v=2.15 m/s.

Barème

Questions posées (hors cours)

Résultats