Thibault Acolas qui réalise un travail sur les propriétés temporelles des cycloïdes m’a posé quelques questions. Cet article essaie d’apporter des éléments de réponse à ces questions.
Thibault Acolas qui réalise un travail sur les propriétés temporelles des cycloïdes m’a posé quelques questions. Cet article essaie d’apporter des éléments de réponse à ces questions.
– Les solutions apportées par de L’Hospital, Newton et Leibniz au problème de la brachistochrone sont-elles les mêmes que celles d’Euler Lagrange et de Jean Bernoulli ?
- La solution du problème de la brachistochrone est unique. Il s’agit d’un arc de cycloïde dont l’extrémité « haute » possède une tangente verticale. Je n’ai pas vu les solutions apportées par les différents auteurs dans les textes originaux mais celles de de L’Hospital et Newton n’utilisent certainement pas la notation mathématique actuelle. Celle de Leibniz en revanche pourrait être plus proche de ce que nous connaissons aujourd’hui car, en 1686 déjà, il écrit l’équation de la cycloïde dans une notation voisine de la notation actuelle.
– Que fait au juste le calcul différentiel dans ce problème et qu’apporte le calcul des variations ?
- Le calcul différentiel s’appuie sur des différences pour lesquelles Leibniz a inventé un langage universel et un symbolisme approprié. Partant de suites, Leibniz utilise x pour représenter l’ordre des termes et y la valeur de chacun des termes. L’idée fondamentale de ce calcul est d’obtenir un rapport de différences
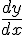 lorsque dx devient très petit. Le problème de la brachistochrone fait intervenir le calcul différentiel et intégral pour calculer un temps de parcours et un calcul des variations pour trouver la valeur minimale de l’intégrale qui donne ce temps de parcours.
lorsque dx devient très petit. Le problème de la brachistochrone fait intervenir le calcul différentiel et intégral pour calculer un temps de parcours et un calcul des variations pour trouver la valeur minimale de l’intégrale qui donne ce temps de parcours.
– D’où vient l’équation d’Euler Lagrange ?
- L’équation d’Euler Lagrange peut s’établir à partir du postulat de Hamilton qui affirme que le mouvement d’un système conservatif depuis l’instant
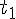 jusqu’à l’instant
jusqu’à l’instant  est tel que la variation de l’intégrale de ligne
est tel que la variation de l’intégrale de ligne 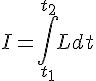 où L est le lagrangien du système, est égale à zéro. Le principe de Hamilton est à la fois une condition nécessaire et suffisante pour l’équation d’Euler Lagrange.
où L est le lagrangien du système, est égale à zéro. Le principe de Hamilton est à la fois une condition nécessaire et suffisante pour l’équation d’Euler Lagrange.
– Quelle est l’interprétation géométrique de l’angle ![]() dans les équations paramétriques de la cycloïde ?
dans les équations paramétriques de la cycloïde ?
- L’angle
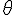 s’interprète facilement si on considère la cycloïde comme la trajectoire d’un point d’un cercle de rayon r roulant sur un plan. En écrivant les équations horaires pour le mouvement du centre du cercle h1(t) et pour la rotation du point autour de ce centre h2(t), on obtient l’équation horaire du point h(t) qui est équivalente aux équations paramétriques de la cycloïde :
s’interprète facilement si on considère la cycloïde comme la trajectoire d’un point d’un cercle de rayon r roulant sur un plan. En écrivant les équations horaires pour le mouvement du centre du cercle h1(t) et pour la rotation du point autour de ce centre h2(t), on obtient l’équation horaire du point h(t) qui est équivalente aux équations paramétriques de la cycloïde :
h1[t_] := {v*t, r}
h2[t_] := r{Cos[omega*t + phi], Sin[omega*t + phi]}
h[t_] := h1[t] + h2[t]N. B. L’angle ![]() permet de fixer la position initiale du point suivi.
permet de fixer la position initiale du point suivi.
L’angle ![]() est l’angle formé par la rayon du cercle avec la verticale.
est l’angle formé par la rayon du cercle avec la verticale.
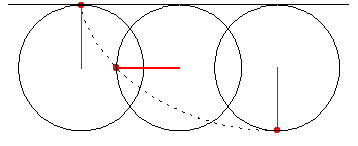
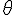 est l’angle entre le rayon du cercle aboutissant à ce point et la verticale. Dans cet exemple,
est l’angle entre le rayon du cercle aboutissant à ce point et la verticale. Dans cet exemple, 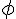 vaut
vaut 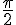 et
et 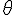 varie de 0 à
varie de 0 à 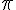
Instructions Mathematica permettant de réaliser une animation
Pour en savoir plus
– Robert Ferréol, Courbe brachistochrone
– Paul Kunkel, The Brachistochrone
– Serge Mehl, Brachistochrone et calcul des variations
