Six exercices sur la relativité restreinte.
par bernard.vuilleumier
Exercice 1
– a) Si ![]() est la longueur d’une règle 1 m dans
est la longueur d’une règle 1 m dans ![]() :
:
-
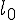 ’ est inférieure à 1 m dans
’ est inférieure à 1 m dans 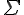 ’ Vrai ou faux ?
’ Vrai ou faux ? -
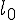 ’ est égale à 1 m dans
’ est égale à 1 m dans 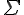 ’ Vrai ou faux ?
’ Vrai ou faux ? -
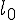 ’ est supérieure à 1 m dans
’ est supérieure à 1 m dans 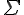 ’ Vrai ou faux ?
’ Vrai ou faux ?
– b) Si ![]() est une durée de 1 seconde dans
est une durée de 1 seconde dans ![]() :
:
-
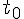 ’ est inférieure à 1 s dans
’ est inférieure à 1 s dans 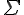 ’ Vrai ou faux ?
’ Vrai ou faux ? -
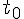 ’ est égale à 1 s dans
’ est égale à 1 s dans 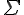 ’ Vrai ou faux ?
’ Vrai ou faux ? -
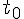 ’ est supérieure à 1 s dans
’ est supérieure à 1 s dans 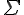 ’ Vrai ou faux ?
’ Vrai ou faux ?
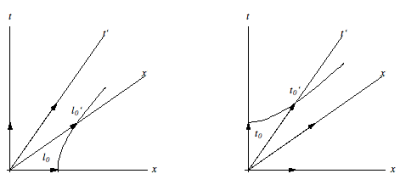
– c) Illustrez par une construction géométrique le fait qu’un observateur de ![]() mesurant la longueur d’une règle en translation à la vitesse
mesurant la longueur d’une règle en translation à la vitesse ![]() arrive à la même conclusion qu’un observateur de
arrive à la même conclusion qu’un observateur de ![]() ’ en translation à la vitesse
’ en translation à la vitesse ![]() mesurant la longueur d’une règle au repos.
mesurant la longueur d’une règle au repos.
– d) Illustrez par une construction géométrique le fait qu’un observateur de ![]() mesurant la durée séparant deux événements qui se produisent au même endroit dans
mesurant la durée séparant deux événements qui se produisent au même endroit dans ![]() ’ en translation à la vitesse
’ en translation à la vitesse ![]() arrive à la même conclusion qu’un observateur de
arrive à la même conclusion qu’un observateur de ![]() ’ mesurant la durée séparant deux événements qui se produisent au même endroit dans
’ mesurant la durée séparant deux événements qui se produisent au même endroit dans ![]() .
.
Exercice 2
Sous l’effet du rayonnement cosmique, une particule prend naissance dans les hautes couches de l’atmosphère et se déplace en direction de la Terre à une vitesse v=0.8 c avant de se désintégrer. Sa durée de vie propre vaut τ=2,6 × 10-8 s.
– a) Construisez la ligne d’univers de cette particule sur un diagramme d’espace-temps attaché à la Terre et calculez sa durée de vie observée depuis la Terre.
– b) Calculez la distance que cette particule franchit dans l’atmosphère entre l’instant de sa création et celui de sa désintégration.
Exercice 3
Un proton se déplace à la vitesse β. Exprimez, puis calculez pourβ=0.987 :
– a) son énergie de masse
– b) son énergie cinétique
– c) son énergie totale.
Exercice 4
Des particules de charge q et de masse m sont accélérées par une tension U.
– a) Exprimez la vitesse de ces particules en fonction de la tension d’accélération et du rapport q/m dans le cadre de la physique classique et dans le cadre de la physique relativiste.
– b) Calculez ces vitesses pour des électrons lorsque U=10000 V ainsi que l’écart relatif entre prédiction classique et relativiste.
Indication : écart relatif en % = 100 ×![]()
Exercice 5
Une particule instable de masse m se désintègre en deux fragments qui s’éloignent respectivement aux vitesses ![]() et
et ![]() . Exprimez les masses de ces fragments en fonction de m,
. Exprimez les masses de ces fragments en fonction de m, ![]() et
et ![]() , puis calculez ces masses pour m=3.67×10-27 kg,
, puis calculez ces masses pour m=3.67×10-27 kg, ![]() =-0.772 et
=-0.772 et ![]() =0.983.
=0.983.
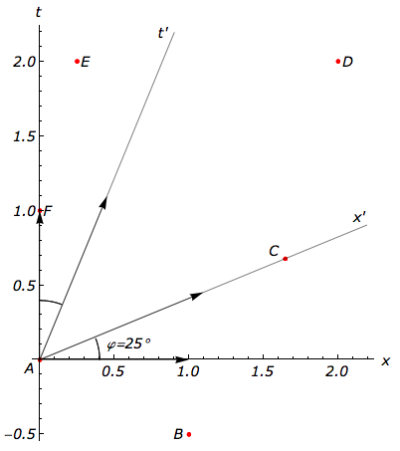
A partir des diagrammes d’espace-temps (x, t) et (x’, t’) ci-dessus, donnez :
– a) la vitesse de translation ![]() des deux systèmes et indiquez son sens dans
des deux systèmes et indiquez son sens dans ![]() et dans
et dans ![]() ’.
’.
– b) la vitesse dans ![]() d’une particule animée d’une vitesse
d’une particule animée d’une vitesse ![]() ’=0.8 selon Ox’ dans
’=0.8 selon Ox’ dans ![]() ’.
’.
– c) les coordonnées des événements B et D dans chacun des systèmes.
– d) les intervalles AD et AE dans les deux systèmes.
– e) Quels sont les événements simultanés dans ![]() ? Et dans
? Et dans ![]() ’ ?
’ ?
– f) Quels sont les événements qui se produisent au même endroit dans ![]() ? Et dans
? Et dans ![]() ’ ?
’ ?
– g) A quelle vitesse ![]() ’ devrait-il se déplacer selon Ox pour que les événements A et B soient simultanés dans
’ devrait-il se déplacer selon Ox pour que les événements A et B soient simultanés dans ![]() ’ ?
’ ?
– h) A quelle vitesse ![]() ’ devrait-il se déplacer selon Ox pour que les événements A et E se produisent au même endroit dans
’ devrait-il se déplacer selon Ox pour que les événements A et E se produisent au même endroit dans ![]() ’ ?
’ ?
Vrai ou faux ?
– A peut causer C
– A peut causer D
– A peut causer E
– B peut causer C
– B peut causer F
– B peut causer A
