Utilisation de ListPlot, Fit, Plot et des commandes TranslateShape, RotateShape, AffineShape du module Shapes.
– Champ
– Documents autorisés : zone personnelle, aide en ligne.
– Lundi 26 mars 2007, CECNB, A3-A4, 95 min.
– Moyenne de classe : 5.03
– Écart type : 0.61
– Effectif : N=15
Problème 1
Un expérimentateur laisse rouler une boule sur un plan incliné. Il mesure, pour différentes inclinaisons du plan, le temps t nécessaire à la boule pour parcourir une distance de 1 mètre, puis il calcule, à partir de ces mesures, l’accélération de la boule. Il obtient les résultats suivants :
| angle en degré | temps en seconde | accélération en m/s2 |
|---|---|---|
| 1 ± 0.2 | 4.18 ± 0.02 | 0.114 ± 0.002 |
| 2 ± 0.2 | 3.09 ± 0.02 | 0.209 ± 0.004 |
| 3 ± 0.2 | 2.51 ± 0.02 | 0.317 ± 0.007 |
| 4 ± 0.2 | 2.21 ± 0.02 | 0.409 ± 0.009 |
| 5 ± 0.2 | 2.00 ± 0.02 | 0.500 ± 0.013 |
Les lois de la mécanique permettent d’établir que, lorsqu’un objet roule sans glisser sur un plan incliné, son accélération est donnée par :
où m est la masse de la boule, r son rayon, I son moment d’inertie, g l’accélération terrestre et ![]() l’angle d’inclinaison du plan.
l’angle d’inclinaison du plan.
Questions
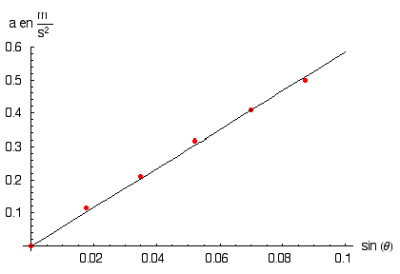
- Reportez les valeurs de l’accélération en fonction du sinus de
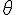 .
. - Ajustez une droite sur les points de mesure.
- Dessinez les points et la droite obtenue sur le même graphique.
- Améliorez la présentation du graphique (voir image)
- Exprimez le moment d’inertie de la boule à partir de la pente de cette droite.
- Calculez le moment d’inertie de la boule à partir de ces mesures.
- Comparez la valeur expérimentale à la valeur théorique (
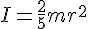 ).
).
Données numériques
– masse de la boule : 1 kg
– rayon de la boule : 3.12 cm
Problème 2
- Dessinez une sphère de rayon unité.
- Dessinez un cône de rayon unité et de demi-hauteur
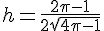 .
. - Enlevez des facettes à la sphère (voir lesquelles sur la figure).
- Emboîtez le cône pour faire coïncider son sommet avec le centre de la sphère.
- Faites subir une rotation à la forme pour que l’axe du cône soit horizontal.
- Animez la figure autour d’un axe vertical passant par le centre de la sphère.

– Points par problème et par question
| Item | points |
|---|---|
| Représentation des points expérimentaux | 2/2 |
| Ajustage d’une courbe sur les points | 2/2 |
| Assemblage des deux représentations | 2/2 |
| Amélioration de la présentation | 2/2 |
| Expression du moment d’inertie | 2/2 |
| Calcul du moment d’inertie | 1/1 |
| Valeur théorique du moment d’inertie | 1/1 |
| Total | 12/12 |
| Item | points |
|---|---|
| Dessin de la sphère | 2/2 |
| Dessin du cône | 2/2 |
| Retrait des facettes | 2/2 |
| Emboîtement du cône | 2/2 |
| Rotation de la forme | 2/2 |
| Animation de la figure | 2/2 |
| Total | 12/12 |
– Barème
Corrigé
Problème 1
– 1. Les points se reportent à l’aide de ListPlot.
– 2. Pour ajuster une droite sur des points de mesure, on utilise Fit.
– 3. Pour dessiner la droite (fonction fournie par l’ajustage) on utilise Plot.
Attention : si vous donnez la fonction Fit comme argument à Plot, vous obtenez des erreurs si vous ne forcez pas l’évaluation de Fit avant celle de Plot avec Evaluate (voir syntaxe dans le code ci-dessous).
– 4. Show assemble plusieurs sorties graphiques. Différentes options permettent d’améliorer la présentation (voir code).
– 5. Le moment d’inertie figure dans la pente de la droite et s’obtient en résolvant par rapport à I l’équation donnant cette pente :
Attention : vous ne pouvez pas utiliser I (i majuscule) pour désigner une variable dans Mathematica car c’est un symbole réservé pour désigner ![]() .
.
– 6. On obtient, en substituant les valeurs numériques dans la solution ![]()
![]()
– 7. La calcul à partir de la formule donnant le moment d’inertie d’une sphère pleine fournit une valeur inférieure et égale à ![]()
![]() .
.
Attention : le rayon s’exprime en m.
Problème 2
– 1. La sphère est une forme prédéfinie du module Shapes.
– 2. Par défaut, le cône Cone[r, h], qui est aussi une forme prédéfinie du module Shapes, a un rayon r=1 et une demi-hauteur h=1. Il faut donc indiquer la demi-hauteur donnée pour obtenir le cône demandé.
– 3. Les facettes s’enlèvent avec Drop (voir syntaxe ci-dessous).
– 4. Pour emboîter le cône et faire coïncider son sommet avec le centre de la sphère, il faut le translater avec TranslateShape de -h selon Oz.
– 5. La rotation s’obtient avec RotateShape[phi, theta, psi]. Les arguments de cette fonction sont les angles d’Euler. N. B. Il y a malheureusement plusieurs conventions pour définir le sens de rotation autour des axes. Mathematica utilise une rotation dans le sens opposé au sens trigonométrique direct. Pour placer la figure dans la position indiquée, il faut lui faire subir une rotation de ![]() selon
selon ![]() et de
et de ![]() selon
selon ![]() .
.
– 6. L’animation s’obtient avec un Table faisant varier l’angle ![]() par pas de
par pas de ![]() de 0 à
de 0 à ![]() .
.
Attention : pour obtenir une taille d’image constante, il faut fixer l’étendue de chaque axe avec l’option PlotRange (voir syntaxe dans le code ci-dessous).
– Figure
– Animation
